Research Accomplishments and Plans of William F. Polik

Overview

The focus of my research program is the experimental and theoretical characterization of molecular potential energy surfaces, with emphasis on energetic and reactive molecules.  While the equilibrium properties of many chemical systems either are already known or may be readily calculated, it is far more difficult to characterize systems away from the harmonic region.  It is essential, however, to characterize the anharmonic properties and behavior of molecules in order to understand and model chemical reactivity.

Accurate determination of potential energy surfaces is among the most important aspects of all chemistry.  Thermodynamic data and kinetic rate constants directly depend on the potential energy surface, and accurate prediction of atmospheric and combustion processes require not only harmonic frequencies but also anharmonic force field and spectroscopic constants.  Current models for protein-folding and other complex biochemical processes were derived from HF/6-31G* potential energy calculations, and the development of improved parameter sets and force fields will require better modeling of the underlying potential energy surfaces.  Accurate modeling of the solar flux and global climate changes requires that anharmonic potential corrections be included when calculating near-IR and visible absorption spectra of water vapor and other greenhouse gases.  The latest quantum chemistry methodologies need to tested and validated with hard-to-obtain experimental data before they can be confidently applied to novel chemical systems.

My research program has made significant and recognized contributions in the area of potential energy surface characterization.  My experimental program has combined lasers, a free jet expansion, and high resolution dispersed fluorescence to invent a new spectroscopic method called Pure Vibrational Spectroscopy, which permits the direct observation of highly excited vibrational energy levels in polyatomic molecules.  Measurement of these vibrational states is the most direct way to experimentally characterize a potential energy surface, as the vibrating nuclei sample the potential energy surface far away from the equilibrium region.  Using this method, my research group has published the most extensive experimental measurements of highly excited vibrational levels in polyatomic molecules.^1-4  These results have led to the most accurate determination of the potential energy surface for a polyatomic molecule to date.⁵

My theoretical efforts are helping to develop and popularize the perturbation-resonance Hamiltonian model for the general analysis of anharmonic resonances in vibrational spectra.^6,7  The extraordinary predictive power of this model allows one to analyze complex spectra with a minimum number of fitting parameters, and the straightforward physical interpretation of the model parameters allows one to immediately identify important energy flow pathways and dynamically conserved quantities in the molecule.  We are also using the most accurate quantum chemistry codes to compute ab initio anharmonic force fields with clusters of computers operating in parallel, and we have developed theoretical methods for calculating spectroscopic model parameters from these force fields.^8,9

Thus, my physical chemistry research program has all the ingredients necessary to characterize Born-Oppenheimer molecular potential energy surfaces:  accurate experimental measurements of vibrational states over a wide energy range, methods for analyzing complex spectra, use of high accuracy ab initio computation, and methods for calculating vibrational energies from potential surfaces.  With these tools in hand, my research program continues to make breakthroughs in the fundamental study of molecular potential energy surfaces and apply the resulting new concepts to chemically important systems.

1.  Pure Vibrational Spectroscopy of Small Molecules

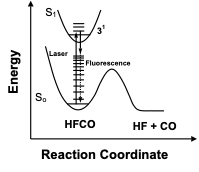
Pure Vibrational Spectroscopy (PVS) is a spectroscopic method for characterizing the vibrational level structure of small molecules at high energies by reducing or completely eliminating rotational congestion.  Sample molecules are cooled in a supersonic expansion, and a low energy rotational level in an excited vibronic state is populated with a laser.  The resulting fluorescence is dispersed with a high resolution monochromator equipped with an intensified charge coupled device detector.  The geometry change accompanying electronic excitation allows access to highly excited vibrational states that would be forbidden in traditional high overtone vibrational spectroscopy.  Strict rotational selection greatly simplify the dispersed fluorescence (DF) spectrum, allowing for unobscured identification of individual vibrational levels similar to Stimulated Emission Pumping (SEP) spectroscopy.  The advantages of DF spectroscopy over SEP are i) DF is a zero background technique and results in a much higher signal-to-noise ratio, ii) DF is not subject to saturation effects and the spectroscopic intensities are consequently much more reliable, and iii) use of an array detector and lack of dye changes results in much more rapid acquisition of spectra (days vs. years).

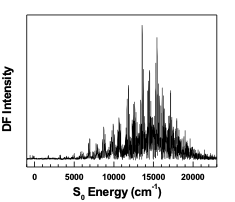
Pure Vibrational Spectroscopy (PVS) Method	PVS Spectrum of HFCO (cover of J. Mol. Spec., November 2001)

Pure vibrational spectra have been recorded and analyzed for formaldehyde¹ (H₂CO), formyl fluoride^2,3 (HFCO), and acetylene^10,11 (HCCH).  In H₂CO 198 newly observed and assigned states have been added to the previously known 79 levels,¹² and in HFCO 338 newly observed and assigned states have been added to the previously known 44 levels,¹³ making these the most extensively characterized four atom molecules to date.  In HCCH, fractionation patterns of zero-order bright states have been analyzed for evidence of intramolecular vibrational relaxation (IVR).  The extent and pathways of IVR to several stretch, bend, and stretch/bend resonances has been determined, providing the most detailed experimental account of energy flow within a four atom molecule to date.^10,11

New PVS studies are being conducted or planned for deuterated analogs of the above systems, D₂CO, HDCO,⁴ and DFCO to study the mechanism of energy flow in molecules.  While the Born-Oppenheimer potential energy surfaces of these systems are identical to the previously studied systems, the isotope difference results in different vibrational level spacing and consequently different anharmonic resonances.  Thus, these spectra will be analyzed for different energy flow pathways and for evidence of vibrationally conserved quantities (see polyad quantum numbers below).  After analyzing a variety of molecular systems experimentally and computationally, we should be able to make generalizations about energy flow mechanisms and predict conserved quantities in molecules.  New PVS studies are also proposed for additional chemical systems (glyoxal, HCCHO, HCP, HNO, ONF), which will extend the range of molecular sizes and atom types under investigation.

2.  Perturbation-Resonance Hamiltonian Models for Energetic Molecules

Understanding intramolecular energy flow, predicting chemical reaction, and influencing the course of a chemical reaction all require that molecules be well-characterized far from their equilibrium configurations.  At large displacement from equilibrium, the potential energy surface of a molecule typically exhibits anharmonicity that shifts and mixes the harmonic oscillator energy levels of the system.  Pure vibrational spectroscopy is a powerful tool for experimentally accessing the potential energy surface at large displacements.  However, theoretical models must account for the extensive state-mixing which is observed in spectra of highly excited vibrational states.

The perturbation-resonance Hamiltonian model is a spectroscopic Hamiltonian that treats nonresonant interactions among harmonic oscillator product basis states using second-order perturbation theory and treats anharmonic resonant interactions explicitly using harmonic oscillator matrix elements.  This hybrid approach is capable of fitting highly excited vibrational states in polyatomic molecules with a minimum number of parameters, each of which has a simple physical interpretation.⁶  Nonresonant perturbative parameters describe the smooth variation of vibrational basis state energy with quantum number, while the resonance parameters account for state mixing.  The scaling laws of harmonic oscillator matrix elements with vibrational quantum numbers allows the perturbation-resonance Hamiltonian to account for extensive vibrational state mixing throughout the entire spectrum with relatively few resonance parameters.  The anharmonic resonance parameters can be related to potential energy force field constants.  The magnitudes of the resonances imply pathways and rates of energy flow within a molecule.  The resonances can also be analyzed for quantities, known as polyad quantum numbers, which are conserved in spite of extensive state mixing.⁷

The observed vibrational state spectrum of H₂CO has been analyzed using perturbation-resonance Hamiltonian models⁷ and fit up to 10,000 cm^-1 with standard deviations of less than 3 cm^-1.  Similarly, the observed vibrational state spectrum of HFCO^2,3 was fit up to 22,500 cm^-1 with standard deviations of about 4 cm^-1.

resonance parameter	Fit 1	Fit 2	Fit 3	Fit 4	Fit 5
k26,5		148.6	146.7	138.6	143.7
k36,5		129.3	129.6	135.1	130.9
k11,55		-140.5	-137.4	-129.3	-127.8
k44,66			-21.6	-23.3	-24.2
k25,35				-18.5	-23.1
k26,36					-5.7
0–10000 cm^-1 fit std. dev. (cm^-1)	23.39	4.34	3.34	2.80	2.76
H2CO perturbation-resonance Hamiltonian fit parameters and results.  As more resonances are included, the quality of the fit improves to the experimental standard deviation.

The perturbation-resonance Hamiltonian model is currently being automated so that it can be applied to a wider variety of chemical systems.  Newly recorded pure vibrational spectra will be analyzed with this model, and general patterns for energy flow pathways will be deduced.  Polyad quantum numbers will be determined for each chemical system.  These quantities have important dynamical consequences by serving to reduce the amount of phase space accessible to a molecule.  By comparing results from several systems, general rules governing accessibility of phase space will be determined and applied to theories of chemical kinetics.

3.  Ab initio Computation of Anharmonic Force Fields

The ab initio computation of anharmonic force fields will serve two very important purposes in my research program.  First, it will guide the initial assignment of experimental spectra.  Second, it will permit the determination of potential energy surfaces in regions where experiments are not yet possible.

While one has been able to compute harmonic force fields with moderate accuracy for some time, challenges remain that limit the ability to accurately compute anharmonic force fields with spectroscopic accuracy (±5 cm^‑1).  First, very high levels of theory and large basis sets must be used to achieve this level of accuracy, e.g., CCSD(T)/aug-cc-pVQZ.  Such calculations require significant computational hardware and require large amounts of computer time.

molecule	cc-pVTZ	cc-pVQZ	aug-cc-pVQZ
H2O	1.5	20	28
H2CO	20	216	551
HFCO	87	862	2200
Minutes per CCSD(T) energy point calculation (Molpro, C1 symmetry; 400 MHz CPU).

Second, while the number of harmonic f_ij force constants scales as N², the number of cubic f_ijk and quartic f_ijkl force constants scale as N³ and N⁴, respectively.  Furthermore, the energy points to compute an nth order force constant by numerical differentiation scales as 2ⁿ.  To illustrate the difficulty in computing higher order force fields, the harmonic force constants of a four atom molecule with 6 vibrational degrees of freedom would require 6²·2²=144 points, whereas the quartic force constants would require 6⁴·2⁴=20,736 points.  Use of symmetry and bookkeeping for duplicative points can significantly lower these numbers, but the strong dependence of computation effort on molecular size and force field order remains.

Computer hardware has become inexpensive enough to permit highly accurate ab initio computation of higher order molecular force fields using state-of-the-art computer codes.  However, the computation of many points at the highest levels of theory still requires significant computation time.

The following approaches are proposed to reduce the computation time required to compute accurate anharmonic force fields:

• Develop efficient bookkeeping procedures to reduce the number of points needed to compute anharmonic force fields, e.g., account for permutations, symmetry, and duplicate geometries.
• Develop hybrid approaches for the harmonic/anharmonic force fields, e.g., aug-cc-pVQZ/cc-pVTZ, as there are reasons to expect that anharmonic force constants converge more rapidly with basis set than harmonic force constants.
• Construct a parallel computing cluster (supercomputer assembled from relatively inexpensive computers) to reduce the compute time for systems from months to days.

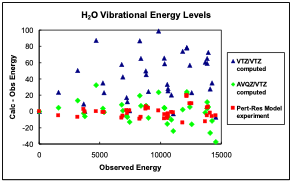
Comparison of low-level (VTZ/VTZ) and hybrid (AVQZ/VTZ) ab initio calculated vibrational energies to experimental energies.

My research program is in a unique position to carry out and assess new computational approaches, as we are conducting experiments that measure large numbers of vibrational energy levels.  After the quartic force fields and accompanying spectroscopic constants are computed for molecules for which extensive vibrational data exists, comparisons between theory and experiment will be made to determine the most accurate methods and to quantify trade-offs between accuracy and speed.¹⁴  Ultimately, the methods developed and validated here will be directly incorporated into the underlying computer codes, so that anharmonic effects on thermodynamic quantities can be automatically computed with conventional programs, e.g., Gaussian, Molpro, Orca, Q-Chem, etc.  We are also developing methods to calculate perturbation-resonance Hamiltonian model parameters from ab initio force fields,⁹ and thereby predict experimental spectra and molecular dynamics directly from ab initio calculations.

4.  Other Research Areas

While characterization of molecular potential energy surfaces is my primary research focus, I am involved in a variety of other areas including:

• The spectroscopic study of rotation-vibration interaction¹⁵
• Energy transfer pathways upon molecular collisions¹⁶
• Photodissociation of metal complexes and product characterization¹⁷
• Cavity ringdown spectroscopy in a free jet expansion to characterize non-fluorescing systems¹⁸
• Visualization of quantum chemistry calculation results¹⁹

I welcome collaborations with colleagues at my home and at other institutions in the above and other areas.

Involvement and Mentoring of Students

My interest in scientific research is driven by two factors:  the advancement of science through new discoveries, and the opportunity to work with students and promote their interest in science.

I have been especially effective at involving undergraduate students in my experimental and theoretical research programs, with between three and five students typically conducting research at any given time.  Each component of my research program illustrates important concepts found in general chemistry, general physics, and physical chemistry.  The research equipment and experimental procedures give students hands-on experience using Nd:YAG and tunable dye lasers, optics, a monochromator, a molecular beam chamber, glass and metal vacuum systems, optical detection equipment, computer interfaces, and electronic signal conditioning equipment.  The theoretical modeling offers mathematically inclined students the opportunity to reach far beyond their formal classroom education.  Students participate in every aspect of the experiment: design, construction, testing, troubleshooting, data acquisition, data analysis, model development, and oral/written presentations, and manuscript preparation.  We hold group meetings in which experimental techniques, related research in the literature, and student results are discussed.  In short, undergraduate students are active participants in all aspects of the scientific method.

There have been 81 undergraduate students in my research program since 1988, of whom 28 are Ph.D. graduates, 11 are M.S. graduates, 10 are M.D.’s, and 4 hold other professional degrees.  Four students have been awarded NSF, DoD, or Hertz predoctoral fellowships, and 4 students were awarded Hope College’s top prize for creativity of independent research.  Of the 63 publications since 1988 that have originated from my work at Hope College, 41 different undergraduate students are co-authors on 30 publications.

I have hosted several international students, worked with two graduate students from M.I.T. during collaborative experiments in my laboratory, and mentored two post-docs.

I receive tremendous satisfaction by sharing my passion to understand chemistry at a fundamental level with my research students in the laboratory.  But the most fulfilling aspect of mentoring students is watching how they succeed in life and surpass me in their accomplishments!

References

1.  R.J. Bouwens, J.A. Hammerschmidt, T.A. Stegink, M.M. Grzeskowiak, P.M. Yorba, and W.F. Polik, "Pure Vibrational Spectroscopy of S₀ Formaldehyde by Dispersed Fluorescence", Journal of Chemical Physics 104, 460 (1996).

2.  K.M. Horsman, T.P. Chassee, and W.F. Polik, "Dispersed Fluorescence Spectroscopy of S₀ Formyl Fluoride Vibrational States", Journal of Physical Chemistry, 104 10070 (2000).

3.  K.E. Hahn, K.M. Horsman, and W.F. Polik, "Characterization of v₃ Vibrational Levels in S₀ Formyl Fluoride using Dispersed Fluorescence Spectroscopy", Journal of Molecular Spectroscopy 210, 98 (2001).

4.  K.K. Ellsworth, B.D. Lajiness, J.P. Lajiness, and W.F. Polik, "Dispersed Fluorescence Spectroscopy of S₀ Vibrational Levels in Formaldehyde-d", Journal of Molecular Spectroscopy 252, 205-213 (2008).

5.  D.C. Burleigh, A.B. McCoy, and E.L. Sibert III, J. Chem. Phys. 104, 480 (1996).

6.  R.W. Field, S.L. Coy, and S.A.B. Solina, Progress of Theoretical Physics Supplement No. 116, 143 (1994).

7.  W.F. Polik and J.R. van Ommen, "The Multi-Resonant Hamiltonian Model and Polyad Quantum Numbers for Highly Excited Vibrational States", Highly Excited States: Relaxation, Reactions, and Structure, edited by A.S. Mullin and G.C. Schatz (American Chemical Society, Washington D.C., 1997) 51-68.

8.  J.L. Davisson, N.R. Brinkmann, and W.F. Polik, "Accurate and Efficient Calculation of Excited Vibrational States from Quartic Potential Energy Surfaces," Molecular Physics, 110, 2587-2598 (2012).

9.  A.M. Rosnik and W.F. Polik, "VPT2+K spectroscopic constants and matrix elements of the transformed vibrational Hamiltonian of a polyatomic molecule with resonances using Van Vleck perturbation theory", Molecular Physics, 112, 261-300 (2014).

10.  S.A.B. Solina, J.P. O’Brien, R.W. Field, and W.F. Polik, "The Acetylene S₀ Surface: From Dispersed Fluorescence Spectra to Polyads to Dynamics", Berichte der Bunsengesellschaft für Physikalische Chemie 99, 555 (1995).

11.  S.A.B. Solina, J.P. O’Brien, R.W. Field, and W.F. Polik, "Dispersed Fluorescence Spectrum of Acetylene from the A ¹A_u Origin: Recognition of Polyads and Test of Multiresonant Hamiltonian Model for the X State", Journal of Physical Chemistry 100, 7797 (1996).

12.  D.E. Reisner, R.W. Field, J.L. Kinsey, and H.-L. Dai, J. Chem. Phys. 80, 5968 (1984).

13.  Y.S. Choi and C.B. Moore, J. Chem. Phys. 94, 5414 (1991).

14.  M.H. Cortez, N.R. Brinkmann, W.F. Polik, P.R. Taylor, Y.J. Bomble, and J.F. Stanton, "Factors Contributing to the Accuracy of Harmonic Force Field Calculations for Water", Journal of Computational and Theoretical Chemistry 3, 1267-1274 (2007).

15.  C.D. Emery, K.S. Overway, R.J. Bouwens, and W.F. Polik, "Dispersed Fluorescence Spectroscopy of Excited Rovibrational States in S₀ Formaldehyde", Journal of Chemical Physics 103, 5279 (1995).

16.  A. K. Chen and W.F. Polik, "K-Rotational Relaxation of S₁ H₂CO (v₄=1, J_KaKc=1₀₁) via Dispersed Fluorescence Spectroscopy", Journal of Physical Chemistry, 100, 10027 (1996).

17.  J.A. Bartz, T.O. Friday, B.R. Goodman, S.E. Kooi, R.G. Blair, and W.F. Polik, J. Phys. Chem. A 102, 10697 (1998).

18.  K.W. Paulisse, T.O. Friday, M.L. Graske, and W.F. Polik, "Vibronic Spectroscopy and Lifetime of S₁ Acrolein", Journal of Chemical Physics 113, 184 (2000).

19.  W.F. Polik and J.R. Schmidt, "Web-Based Computational Chemistry Calculations in Education and Research", WIREs Computational Molecular Science, 12:1, 1-22, e1544, (2021).