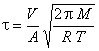LOW-PRESSURE EFFUSION
OF GASES
1. Purpose
The purpose of this experiment is to compare the effusion rates of different gases. Specifically, the effusion rates of helium, nitrogen, and argon are measured. The molar mass of the gases are determined using the Kinetic Theory of Gases, and the Graham's Law of Effusion is tested. In addition, experience is gained using a high vacuum system.
2. Apparatus
The system consists primarily of a 5 L roundbottom flask. Gas is admitted to the system through an expansion filling system. This gas effuses from the system through a 200mm diameter pinhole. A high vacuum is maintained outside of the system, with an oil diffusion pump, liquid nitrogen trap, and rotary oil pump.
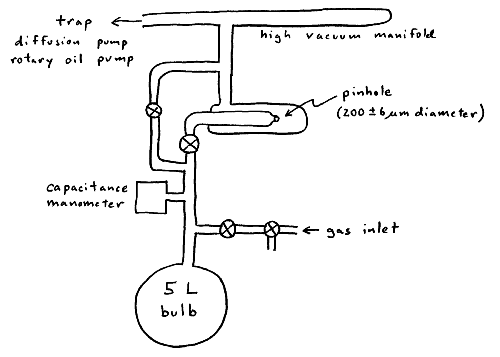
A capacitance manometer measures the system pressure. A flexible membrane with the manometer is depressed by pressure, changing the value of a capacitor in an electronic circuit. A transducer converts this capacitance change into a DC voltage, which is monitored with a stripchart recorder.
3. Effusion
Two conditions must be met for true effusion to occur.
First, the mean free path l of the gas in the system must be greater than the pinhole diameter. This implies that an escaping molecule encounters no other molecules as it exits the pinhole. Molecules act independent of each other as they leave the system through the pinhole, i.e., they undergo molecular flow, as opposed to viscous or turbulent flow.
Second, the system pressure is much greater than the manifold pressure. This implies that backflow from the manifold into the system can be neglected.
If these two conditions are met, then one can assume that the rate of effusion equals the rate at which molecules strike the pinhole area.
4. Calculation of Effusion Rate
The effusion rate is calculated from the kinetic theory of gases by assuming that every molecule that strikes the pinhole area escapes from the system. This calculation proceeds in four steps: 1) the collision frequency of molecules with the wall, 2) the number of molecules escaping the system per unit time, 3) the change in system pressure per unit time, and finally 4) the system pressure as a function of time.
4. A.
Wall collision rate, Z
A molecule traveling with velocity vx will strike a wall within time Dt only if it is closer than distance vx·Dt to the wall.
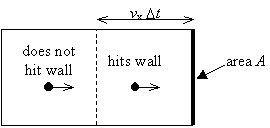
Thus, the number of wall collisions for molecules traveling with velocity vx is
![]()
where N/A is the number density of the molecules and A is the wall area.
Since there is a distribution of molecular velocities, this expression must be integrated over the velocity distribution function f(vx)
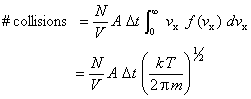
The number of wall collisions per unit time and area is the wall collision rate Z, which can be calculated by
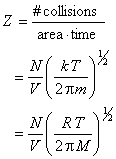
where the last step recognizes that R = k Na and M = m Na.
For an ideal gas
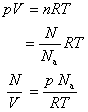
Thus,
|
|
4. B.
Effusion rate, -dN/dt
If one assumes that effusion occurs every time a molecule strikes the area of the pinhole, the effusion rate (loss of molecules per unit time) equals the wall collision rate times the area of the pinhole
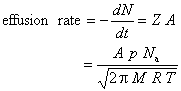
This last equation implies Graham’s Law
|
|
which states that the effusion rate is inversely proportional to the square root of molar mass. Note that this inverse square root dependence arises from the velocity distribution of gas molecules.
4. C.
Effusion rate, -dp/dt
Since it is more convenient to measure system pressure than count the number of molecules in the system, the effusion rate in terms of N is converted to an effusion rate in terms of p.
The change in N is related to the change in p by
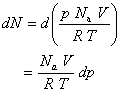
Thus,
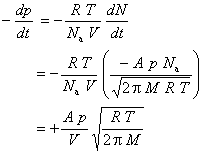
This differential rate law can be rearranged to
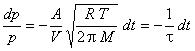
where
|
|
is the “relaxation time”, “decay time”, or “1/e time” for the system.
4. D.
System pressure, p(t)
Sine pressure is measured as a function of time, the differential rate law is integrated to yield the integrated rate law
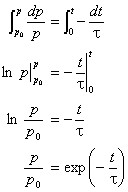
Thus
|
|
5. Data Treatment
5. A.
Typical data
Since voltage produced by the capacitance manometer is proportional to pressure, one has
![]()
where V is the capacitance manometer voltage at time t and V0 is the initial capacitance manometer voltage.
Typical data recorded for this experiment would look like a single exponential decay characterized by decay time t.
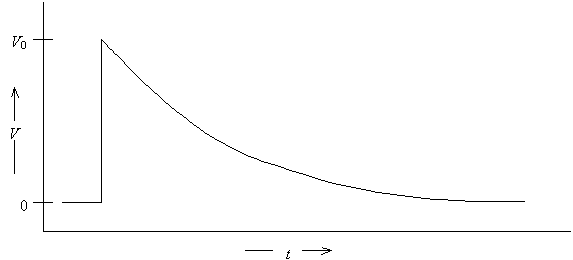
5. B.
Determination of decay time, t
Several methods exist to calculate or approximate the decay time t of a single exponential decay.
· The data can be linearized and fit to a straight line
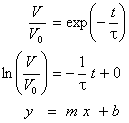
[Figure]
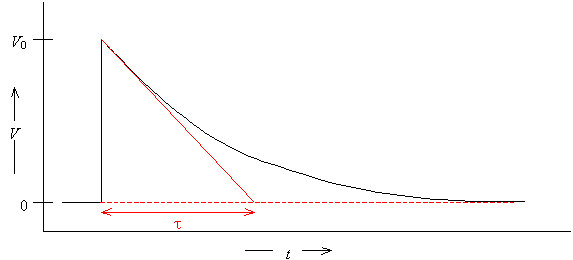
· The initial slope can be extrapolated to the baseline. If the data is a single exponential, it will intersect the baseline at time t.
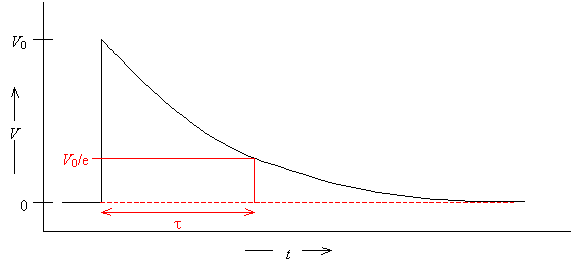
· The “1/e” time can be calculated. If the data is a single exponential, the “1/e” time occurs at time t. Thus, t is the time needed for the signal to decay to 37% of its original height.
![]()
5. C.
Calculations
The system constant V/A is determined from calibration runs using the measured relaxation time t and the known molar mass M of nitrogren
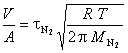
The molar masses of helium and argon are then determined using the measured relaxation time t and the previously determined system constant V/A.
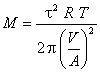
Observe that units work out properly
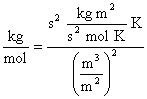
where it has been recognized that J = kg·m2·s-2.
5. D.
Limitations of data linearization
Linearizing data can lead to difficulties in data analysis because real data has noise superimposed on the actual signal.
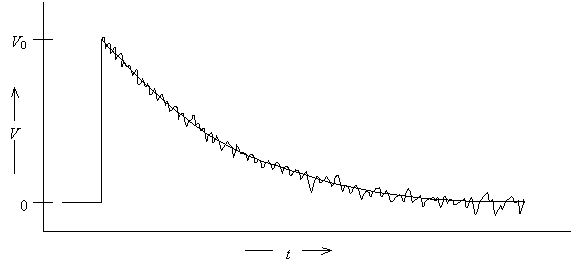
Since ln is a nonlinear function, noise that was independent of signal height will depend on signal height after transformation.
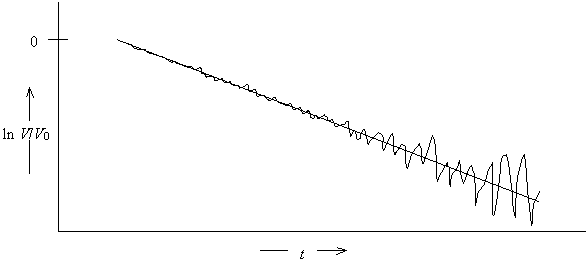
Thus, linearization of the data leads to two problems for data analysis
· Some of the data points near the baseline will be negative. The logarithm of a negative number is undefined, leading to an error in the computerized analysis of the data.
· The assumption of equal uncertainty for all data points is not valid for the linearized data.
Linearization of the data works in the current experiment because the data is relatively noise free and data is recorded only until the signal reaches about one-third of the original height. However, nonlinear fitting programs, e.g., use of Excel’s solver, may be required for other experiments in which data is being fit to a nonlinear function.