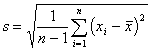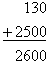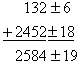DATA ANALYSIS

1. Error

1. A. Error is always present

Scientific experiments are carried out to measure quantities of interest and to develop and test theories.

Error is present in all experiments and prevents one from obtaining the "true value" of any measurable quantity.

Although the true value of a quantity is unknowable due to error, well-defined bounds can be placed on experimental uncertainty.

1. B. Terminology about errors

Systematic Error	Reproducible inaccuracy (always the same sign and magnitude); can be discovered and corrected in principle
Random Error	Indeterminate fluctuations (positive and negative); can be reduced by averaging independent measurements
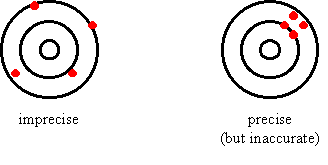
Accuracy	Nearness to "truth"; depends on how well systematic errors are controlled or compensated for
Precision	Reproducibility; depends on how well random error can be overcome

Pictorial Example:

From the above definitions, it is seen that

· Minimizing systematic error increases the accuracy of a measurement

· Minimizing random error increases the precision of a measurement

Example: The Hubble telescope was precise (flat to l/50) but inaccurate (focal length error of 1 mm). However, since the error was systematic, NASA was able to correct it with compensating lenses.

2. One-Dimensional Measurements

One-dimensional measurements are measurements of a value of a physical property. A data set consists of a set of repeated measurements, {x₁, x₂, ..., x_n}. An example is the determination of the mass of a sample by several weighings.

2. A. Distribution of one-dimensional measurements

Repeated experiments will yield a histogram of measurements centered about an average value (mean) with a characteristic spread (standard deviation). In the limit of an infinite number of measurements, the probability distribution is observed to be a Gaussian distribution (or normal error distribution).

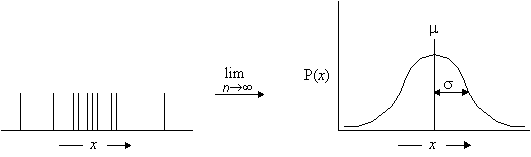
68% of the area under a Gaussian distribution lies between ±1s; 95% of the area lies within ±2s.

2. B. Parent distribution

The parent distribution is the “true” distribution obtained from an infinite number of measurements.

parent mean:
parent standard deviation:

The mean m the distribution is the average value. The standard deviation s is the square root of the average squared deviation from the mean.

2. C. Sample distribution

The sample distribution is an observed distribution obtained from a finite number of measurements.

sample mean:
sample standard deviation:

One “degree of freedom” is used to determine the mean of the distribution; hence, the divisor is n-1 in the sample standard deviation.

Note the use of greek letters for the parent distribution and roman letters for the sample distribution.

2. D. Reporting values

When reporting values, always report the mean, standard deviation, and units:

Use two significant figures for s and match precision for .

Example: l = 12.5 ± 1.3 mm. Note that the mean has three significant figures and the standard deviation has two significant figures; however, the precision of both quantities is 0.1 mm.

2. E. Significant figures

Use of standard deviations can be thought of as “advanced significant figure theory” because the standard deviation specifies the uncertainty in a value more precisely. We will also see that there are methods to propagate uncertainty during calculations.

Preview:

3. Two-Dimensional Measurements

Two-dimensional measurements are measurements that describe how one physical property depends on another. A data set consists of (x,y) pairs, {(x₁,y₁), (x₁,y₁), ..., (x_n,y_n)}. For example, a set of (T,p) data points describes how pressure depends on temperature.

3. A. Linear least square fitting

Linear least squares fitting is a method which finds the best straight line fit to a set of (x,y) data points, i.e., finds the slope m and intercept b of the function mx+b which best fits the observed data. (Actually the method finds the best fit values for parameters which appear linearly in the fitting function, but a straight line is the most common case.)

3. B. Derivation of the least squares best fit for a straight line

If 1) the parent distribution is linear, e.g., a straight line, 2) the parent distribution is Gaussian, and 3) all standard deviations are equal, then the best fit of the data {(x₁,y₁), (x₁,y₁), ..., (x_n,y_n)} is obtained by minimizing the sum of squared differences between the observed data and predicted fit

If the fitting function is a straight line

then the residual may be written as

R is minimized with respect to variations in fitting parameters m and b by setting its partial derivatives equal to zero

Evaluating these derivatives yields

which can be simplified by dividing by -2, separating the summations, and recognizing that S1=n

This leaves two equations and two unknowns. Solving for m and b yields

where

Furthermore, the standard deviations may be shown to be

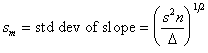
Observe that two “degrees of freedom” are used to determine the slope and intercept of the fitting function; hence, the divisor is n-2 in the standard deviation of the fit.

3. C. Using the least squares best fit formulas

In practice, one uses a computer program or spreadsheet to accumulate the summations

and then calculate

The units of m and s_m are the units of the slope, i.e., the y units divided by the x units. The units of b, s_b, and s are the same as the y units.

3. D. Intuitive definitions of s, s_m, and s_b

The following figure shows the best fit to a set of data points as a solid line. Two limiting “reasonable” fits are also shown as dashed lines.

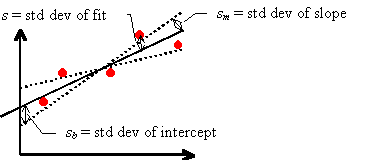
The standard deviation of the fit s is approximately the average difference in y between each data point and the best fit line. The standard deviation of the slope s_m is approximately the difference in slope between the best fit line and a limiting reasonable fit line. The standard deviation of the intercept s_b is approximately the difference in the y-intercept between the best fit line and a limiting reasonable fit line.