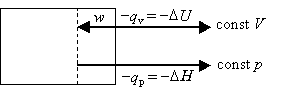BOMB CALORIMETRY
1. Purpose of Bomb Calorimetry Experiments
Bomb calorimetry is used to determine the enthalpy of combustion, DcombH, for hydrocarbons:
CxHYOz
(s) + (2X+Y/2-Z)/2 O2 (g) ® X CO2
(g) + Y H2O (l)
Since combustion reactions are usually exothermic (give off heat), DcombH is typically negative. (However, be aware that older literature defines the "heat of combustion" as -DcombH, so as to avoid compiling tables of negative numbers!)
2. Construction of a Bomb Calorimeter
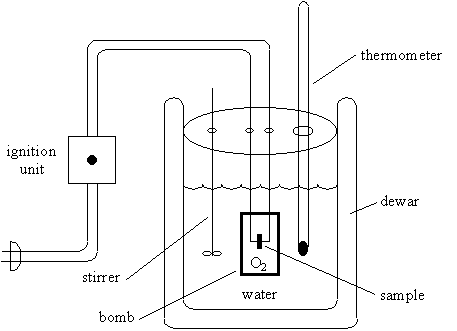
The bomb calorimeter consist primarily of the sample, oxygen, the stainless steel bomb, and water.
The dewar prevents heat flow from the calorimeter to the rest of the universe, i.e.,
qcalorimeter = 0
Since the bomb is made from stainless steel, the combustion reaction occurs at constant volume and there is no work, i.e.,
wcalorimeter = -ò p dV = 0
Thus, the change in internal energy, DU, for the calorimeter is zero
DUcalorimeter = qcalorimeter + wcalorimeter = 0
The thermodynamic interpretation of this equation is that the calorimeter is isolated from the rest of the universe.
3. DU and DH in a Bomb Calorimeter
3. A. Internal energy change DU
Since the calorimeter is isolated from the rest of the universe, we can define the reactants (sample and oxygen) to be the system and the rest of the calorimeter (bomb and water) to be the surroundings.
The change in internal energy of the reactants upon combustion can be calculated from
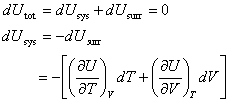
Since the process if constant volume, dV=0. Thus, recognizing the definition of heat capacity Cv yields
![]()
Assuming Cv to be independent of T over small temperature ranges, this expression can be integrated to give
|
|
where Cv is the heat capacity of the surroundings, i.e., the water and the bomb.
3. B. Enthalphy change DH
By definition of enthalpy
![]()
Since there is very little expansion work done by condensed phases, D(pV) » 0 for solids and liquids. Assuming the gas to be ideal yields
|
|
3. C. Intuitive difference between DU and DH
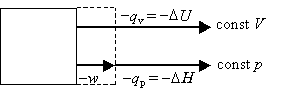
Recall that DU=qv is the heat flow under constant volume conditions, whereas DH=qpis the heat flow under constant pressure conditions. The difference between these two situations is that pV work can be done under constant pressure conditions, whereas no pV work is done under constant volume conditions.
Consider the case where Dngas > 0. i.e., the system expands during the reaction. The same amount of energy is released by the reaction under both sets of conditions. However, some of the energy is released in the form of work at constant pressure; thus, the heat released will be less than at constant volume. Mathematically,
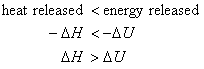
In the case where Dngas < 0. i.e., the system contracts during the reaction, the surroundings does work on the system. Thus, this work is available for energy release from the system back to the surroundings in the form of heat. Mathematically,
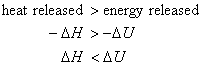
These cases can be depicted pictorially as follows:
|
|
Dngas > 0 work done by system -DH < -DU or DH > DU |
|
|
|
|
|
|
|
Dngas < 0 work done on system -DH > -DU or DH < DU |
|
4. Calibration of the Calorimeter
4. A. Estimating Cv
The heat capacity of the bomb calorimeter can be estimated by considering the calorimeter to be composed of 450 g water and 750 g stainless steel. Knowing the specific heat capacity of water to be 1 cal/g·K and estimating the specific heat capacity of steel to be 0.1 cal/g·K yields
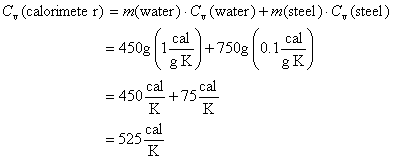
4. B. Measuring Cv
For accurate work, the heat capacity of the calorimeter must be measured. This is done by depositing a known amount of energy into the calorimeter and observing the temperature increase. The two most common methods for measuring Cv are
1. Burning a standard with known DU, e.g., benzoic acid.
|
|
mbenzoic acid DUbenzoic acid = mbenzoic acid -6318 cal/g·K = -Cv DT |
2. Doing electrical work by passing current though a resistor.
|
|
DU = w + q = V·I·t + 0 = Cv DT |
5. Corrections in Bomb Calorimetry
5. A. Combustion of fuse
Nickel and iron fuses can burn according to
Ni + ![]() O2 ® NiO
O2 ® NiO
or
2Fe + ![]() O2 ® Fe2O3
O2 ® Fe2O3
The heat released by combustion of the fuse is accounted for by recognizing that
|
|
DU = DUsample·msample + DUburned fuse·mburned fuse = -Cv DT |
where the mass of the burned fuse is determined by weighing the fuse before and after firing the bomb.
5. B. Nonadiabaticity of calorimeter
A bomb calorimeter is only approximately adiabatic. In reality, there is a small heat leak through the dewar (qcalorimeter ¹ 0) and the stirrer does work on the calorimeter (wcalorimeter ¹ 0). Nonadiabaticity is corrected for with an empirical radiative correction, RC.
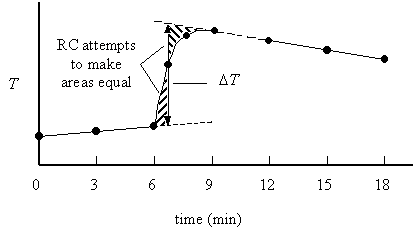
The time at which the bomb is considered to be fired is the time that makes the areas indicated in the above figure equal. For the Parr calorimeter, this is estimated to be at t = 7 minutes. Thus, the temperature at t = 6 minutes must be extrapolated forward 1 minute by the pre-firing slope, and the temperature at t = 12 minutes must be extrapolated backward 5 minutes by the post-firing slope. Mathematically, this is done as follows
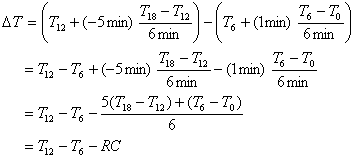
5. C. Nitric acid formation
At high temperatures, nitrogen can form nitric acid in the presence of oxygen and water. (This reaction also occurs in automobile engines and is partially responsible for smog production.)
N2 + ![]() O2 + H2O ®
2HNO3
O2 + H2O ®
2HNO3
Flushing the bomb with oxygen prior to firing, thereby displacing all nitrogen, eliminates nitric acid formation.
6. Application of DcombH
In addition to measuring the energy release of one particular reaction, calorimetry is an important tool for determining the enthalpy of formation for the compound under study. This information can then be applied to any reaction involving the compound.
The enthalpy of combustion for the reaction
can be written as
|
DcombH(CxHyOz) = |
v(CxHyOz)DfH°(CxHyOz) + v(O2)DfH°(O2) + |
DcombH(CxHyOz) = v(CxHyOz)DfH°(CxHyOz) + v(O2)DfH°(O2) + v(CO2)DfH°(CO2) + v(H2O)DfH°(H2O)
where v(i) is the stoichiometric coefficient of i. Since DfH°(CxHyOz) and DfH°(H2O) are known (and DfH°(O2) equals zero), measurement of DcombH(CxHyOz) allows calcualtion of DfH°(CxHyOz).
7. Other Types of Calorimeters
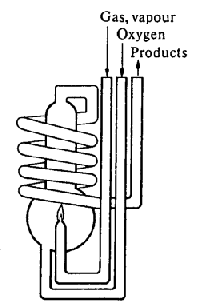
There are many kinds of calorimeters, each designed for measuring the heat released by a particular chemical process. Some examples include:
|
|
Flame Calorimeter The combustible gas is metered into the calorimeter. Temperatures of all reactants must be controlled. Since the reaction occurs at constant pressure, DcombH is measured directly. |
|
|
|
|
|
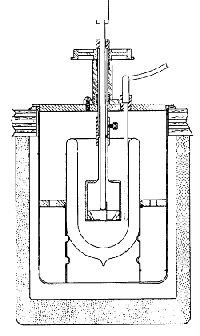
Solution
Calorimeter Reactants are initially separated. The temperature change is measured when they are allowed to mix. Quantities that can be determined include DmixH, DdilutionH, and DsolvationH. |
Calorimeter design is very tricky, especially for processes involving very small energy changes, e.g., protein folding, or energy changes on top of a large background, e.g., excess heat from "cold fusion". Heat leaks must be minimized, and all other heat generating processes must be accounted for.