CHEMICAL KINETICS

1. Reaction Rate

Observe that use of the stoichiometric coefficient insures that the rate of a chemical reaction is the same regardless of which chemical species is used in the definition. In the above example, 1 molecule of A is consumed for every 3 molecules of C created; however, the reaction rates are equal due to inclusion of the stoichiometric coefficient.

2. Rate Law

where k is a rate constant, m is reaction order with respect to A, n is the reaction order with respect to B, and m+n is the overall reaction order.

The rate constant is independent of the concentrations of the chemical species involved in the reaction. However, it depends on other factors such as temperature or ionic strength, e.g., k(T).

The units of the rate constant depend on the overall reaction order. The can be deduced by recognizing that Rate has units of concentration per time. Concentration is usually measured in molarity (M) for solution reactions and in molecules/cm³ for gas phase reactions.
 

Example: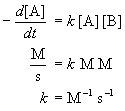

In general, the form of the rate law is NOT determined by the reaction stoichiometry, but is determined by the reaction mechanism.
 

Example:	Br2 + I2 ® 2BrI which reacts by a one-step mechanism
Example:	Br2 + H2 ® 2HBr which reacts in a complicated mechanism in which the product, HBr, can react with a reactant, Br2.

Rate laws are expressed as the differential of concentration with time, whereas experimental measurements are usually concentrations. Thus, in order to match theory with experiment, either the rate law must be integrated or the data must be differentiated.

3. Chemical Kinetics

• Experimentally measure rates of important chemical reactions to understand complex chemical systems. Current examples of important fields in chemical kinetics include:
• Combustion and atmospheric chemistry (gas phase).
• Biochemical pathways and polymer synthesis (liquid phase).
• Semiconductor and superconductor sythesis (solid phase).
• Experimentally determine rate laws, and suggest possible mechanisms that are consistent with the observed rate law.
• Measure dependence of rate constant on other experimental variables:
• Temperature: All reaction rates depend on temperature.
• Pressure: Gas phase reactions, e.g., O + O₂ ® O₃, depend on overall pressure. Changes in the stability of solid phases will lead to different reaction rates at different pressures.
• Ionic Strength: Electron and proton transfer rates of biochemical reactions depend on pH.
• Use kinetic data to characterize the energy and composition of the "transition state" in a chemical reaction.

4. Bromination of Acetone

is known to be acid-catalyzed. Thus, the following form of the rate law is assumed

Bromine is a reddish-brown, and all the other reactants and products are clear. Thus, the reaction rate is conveniently measured by monitoring the concentration of bromine with a spectrophotometer.

The form of the rate law can be simplified by arranging the experimental conditions so that the concentration of one species is much smaller than the others, a technique known as "flooding". The concentration of the other species therefore remain essentially constant during the course of the reaction.

In this case, [Br₂] << [CH₃COCH₃], [H⁺]. Thus the rate law reduces to

where

The exponent q can be determined by measuring the concentration of bromine [Br₂] as a function of time t and comparing the observed data to the integrated rate laws for various values of q:

Order (q)	Differential Rate Law	Integrated Rate Law
0
1
2

The rate constant k is then determined for each reaction run through the definition of k_obs.

5. Reaction Mechanism

Example: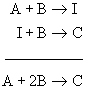

The bromination of acetone is a reaction for which the first step is believed to be the rate limiting step. Thus, the form of the rate law predicts the first step of the reaction mechanism.

It is generally true that the molecularity of the transition state can be determined from the form of the rate law. See Espenson, "Chemical Kinetics and Reaction Mechanism", McGraw-Hill, 1981, p. 90 for a very readable discussion on this topic.

Note that it is usually the case that the rate law is known from experiment and that the elementary steps must be postulated so as to be consistent with the observed rate law. It is for this reason that it is not possible to "prove" a mechanism using kinetics. Rather, reasonable mechanisms are put forward, and kinetic experiments are designed to distinguish among them.

6. Temperature Dependence

The values of A and E_a can be determined by linearizing the Arrhenius equation

A plot of ln k versus 1/T will have a slope of -E_a/R and an intercept of ln A.

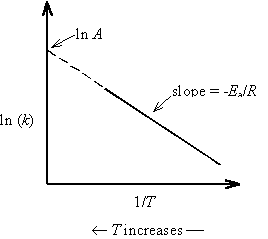
In the collision theory of bi-molecular gas phase reactions, the frequency factor A is interpreted as the frequency of encounters among reactants irrespective of energy. The activation energy E_a is the minimum energy reactants must possess in order to form products. The Boltzmann distribution predicts that the exponential function in the Arrhenius equation is the fraction of collisions with energy greater than E_a. The product of the frequency factor and the Boltzmann exponential functions therefore gives the reaction rate constant. There is an analogous interpretation of these terms for reactions that occur in solution.

In light of the collision theory interpretation, the activation energy E_a is also often interpreted as the energy of the transition state relative to the reactants.

Collision theory is the most simple model of chemical kinetics. Reactions involving free radicals or stable intermediates are known to display Arrhenius plots with negative values of E_a! The interpretation of activation energy as the energy of the transition state is not applicable in these cases, as the actual kinetics is much more complex than the collision theory model.

7. Exercise

• Report the authors, title, and full reference of the article.
• What chemical reaction is under study?
• What experimental technique is used to measure the reaction rate?
• What is the rate law for the reaction?
• What is the rate constant (with proper units)?
• Discuss why knowledge of the rate of this reaction is important or interesting.