Fluid flow through pipes is of immense importance to chemical engineers, who must design appropriate methods for transporting chemicals to and from reaction vessels. Viscosity of fluids is the key physical property that dictates the design of pipelines to transport material. Thus, an understanding of liquid and gas viscosity is essential for engineering a chemical process.
The viscosity of gases played an important role in the historical development of the kinetic theory of gases (see Keith J. Laidler, The World of Physical Chemistry, Oxford University Press, 1993, p. 150-154). James Clerk Maxwell, who is famous for the Maxwell-Boltzmann distribution of molecular velocities and Maxwell's Equations of electromagnetic radiation, proposed in 1860 that gases possess a distribution of velocities. Although now fully accepted, this proposal went against the conventional theory of the time that a range of velocities would be equalized by molecular collisions. He was troubled with his own proposal, however, because it had "the curious result" that viscosity is independent of pressure which was "certainly very unexpected." Maxwell and his wife made the first reliable measurements of gas viscosities in order to determine the dependence of gas viscosity on temperature and pressure. These measurements were made using an apparatus in attic of their house, and the temperature was controlled through appropriate stoking of the fireplace. The results were reported in 1866, reconciling his kinetic theory of gases with observed gas viscosities.
As an aside, Maxwell was never able to reconcile his kinetic theory of gases with the observed ratio of specific heats, Cp/Cv, for diatomic gases. A diatomic molecule has three translational, three rotational, and one vibrational degree of freedom. Translational and rotational degrees of freedom each contribute 1/2 R to the specific heat, and vibrational degrees of freedom contribute R to the specific heat. Since Cp = Cv + R, the ratio of specific heats was predicted to be (3/2R + 3/2R + R + R) / (3/2R + 3/2R + R) = 5R / 4R = 1.2, which differed from observed values for oxygen, hydrogen, and nitrogen of about 1.4. As a result, Maxwell proclaimed that the kinetic theory "could not possible satisfy the known relation between the two specific heats of a gas" and "the result of the dynamical theory, being at variance with experiment, overturns the whole hypothesis, however satisfactory the other results might be." Despite considerable effort, Maxwell was never able to reconcile the kinetic theory of gases with the specific heats experimental result. This required the advent of quantum mechanics, which explained that the degrees of freedom for molecular vibration and rotation around the axis of a linear molecule were to be neglected because the excited quantum states for these motions were too high in energy to be accessed at room temperatures. Thus, the ratio of specific heats should be (3/2R + 2/2R + R) / (3/2R + 2/2R) = (7/2R) / (5/2R) = 1.4, which is in very close agreement with experiment.
Both gas effusion and gas viscosity experiments validate the kinetic theory of gases and provide access to microscopic information from macroscopic measurements. The rate of gas effusion provides a means of determining the average molecular velocity, as faster molecules will strike the pinhole area more frequently and therefore effuse more rapidly. The viscosity of a gas provides a means for determining molecular diameters, as viscosity arises from collisions among molecules.
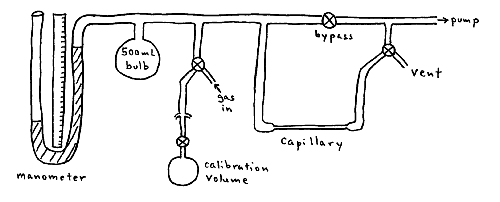
A gas sample is drawn through a thin capillary tube. The change in pressure of the system is measured with a manometer as a function of time. A calibration flask of known volume is provided to determine the volume of the system.

In order to measure gas viscosities, laminar flow is assumed in the capillary. Laminar flow implies that the gas flows in "layers" such that each layer moves at a velocity infinitesimally different than the layers adjacent to it.
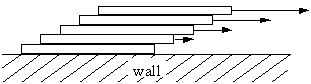
Since the wall is stationary, the layer along the wall has a velocity of zero. The fluid flows more quickly the further away it is from the stationary wall. Laminar flow is commonly experienced in smooth streams and rivers, where water flows slowly along the banks and rapidly in the center.
Adjacent laminar sheets experience friction as they slide past one another. This frictional force is proportional to the area A of contact between the sheets and the velocity gradient dv/dr
|
|
The proportionality constant h is called the viscosity coefficient. The units of h can be determined from unit analysis on its defining equation. In the cgs (cm-gram-second) unit system
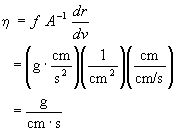
In honor of Poiseville, the cgs unit of viscosity is called a poise
|
|
The derivation of the gas viscosity equation will proceed in four steps:
Consider an incompressible fluid flowing through a circular tube with radius R and length l. The fluid at the walls of the tube is assumed to be stationary, and the flow rate increases to a maximum at the center of the tube.
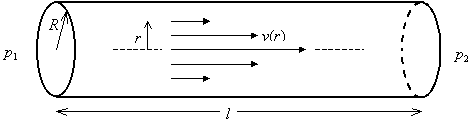
Consider the forces acting on a cylinder of radius r as it moves through the tube at velocity v. The frictional force fr acting along a cylinder of fluid of radius r and length l is
![]()
where h is the viscosity coefficient, 2prl is the surface area of the cylinder, and dv/dr is the velocity gradient. Note that dv/dr < 0 because r is measured from the center of the tube. The driving force fd on the cylinder is
![]()
where p1 is the fore pressure, p2 is the back pressure, and pr2 is the area of the cylinder end.
Under steady flow conditions, the forces must exactly balance each other
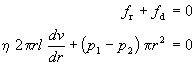
Separating variables
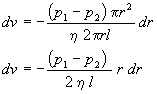
and integrating from the wall (v=0 at r=R) of the cylinder toward the center(v at r)
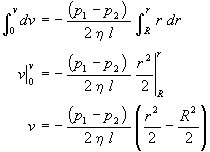
yields the velocity of the fluid as a function of position within the tube
|
|
Note that the fluid velocity is zero at the tube wall (r=R) and is a maximum at the tube center (r=0). The r2 dependence of v implies that the velocity profile looks like a parabola.
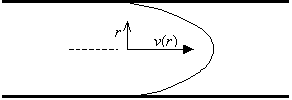
The total volume of fluid flowing through the tube per second dV/dt is calculated by integrating the fluid velocity v over each element of cross-sectional area 2prdr.
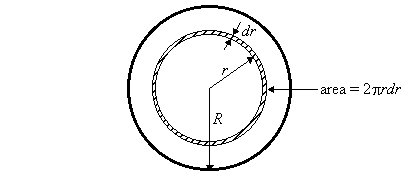
Thus,
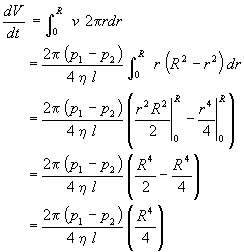
which upon rearrangement yields
|
|
This is Poiseville's equation, which applies to incompressible fluids undergoing laminar flow. Poiseville's equation may be satisfactorily applied to liquids but not to gases, as volume is a strong function of pressure for gases.
Three approximations are made to apply Poiseville's equation to gases.
First, since the volume of a gas depends on pressure, the average pressure p0 is used.
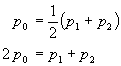
Second, the gas is assumed to be ideal in order to calculate the moles of gas flowing through the tube per second.
![]()
Thus,
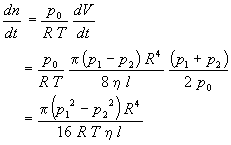
Third, since p1 is the pressure of the system at the capillary inlet measured with the manometer and p2 is the pressure at the capillary outlet maintained with a rotary oil pump, then it is a good approximation that p1>>p2. Thus, p22 can be neglected relative to p12 in the previous equation yielding
![]()
An experimental determination of gas viscosity usually involves measurement of pressure change with time in a constant volume system. Using the ideal gas law to relate change in pressure to change in moles gives
![]()
where p1 is the system pressure, V is the system volume, and the negative sign indicates that the system pressure decreases as gas flows through the capillary. Thus,
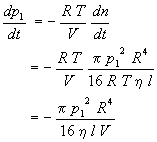
Since pressure is measured as a function of time, the preceding equation must be integrated. Separation of variables yields
![]()
which can be integrated from the initial pressure p1=pi at time t=0 to the pressure pi at time t
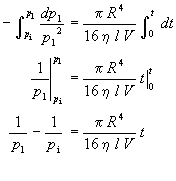
which upon rearrangement yields
|
|
where p1 is the system pressure, R is the capillary radius, h is the viscosity coefficient, l is the capillary length, V is the system volume, t is time, and pi is the initial system pressure at t=0.
Note the R4 dependence of the flow rate in the gas viscosity equation. One application of the strong dependence of flow rate on capillary radius is the use of nitroglycerin to increase the radius of blood vessels, i.e., as a vasodilator, and thereby decrease the resistance to flow. Nitroglycerine very effectively relieves chest pain due to poor circulation and is an alternative to bypass surgery for the eldery.
The gas viscosity equation is of the form y = mx + b. Thus, a plot of 1/p1 against t will have a slope of pR4/16hlV. Measurement of the slope and knowledge of the system volume, capillary radius, and capillary length will permit the determination of gas viscosity h. Such a plot typically has the following appearance
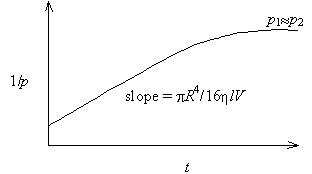
Note that at large t the plot flattens out. This occurs because p1» p2 at long times, and p22 can no longer be neglected.
Observe that the slope of such a plot has units of Torr-1·sec-1, which are neither SI nor cgs units. A convenient method for converting pressure units into SI or cgs units is to take the ratio of the two common values of the gas constant, R = 8.314 J·K-1·mol-1 = 0.08206 L·atm·K-1·mol-1.
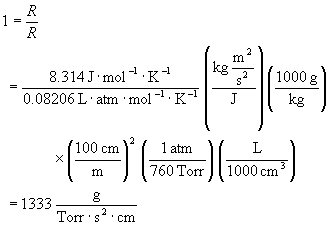
Units of poise are commonly used for viscosity coefficients because the resulting values are near one. Typical values for several substances are as follows
|
substance |
h (poise) |
|
oil |
~ 1 |
|
water |
~ 10-2 |
|
gas |
~ 10-4 |
Thus, gas viscosities are often reported as hundreds of micropoise.
The kinetic theory of gases relates gas viscosity coefficient h to molecular diameter by
|
where
|
s
is the collision cross-section of the molecule, and d is molecular diameter. (Recall that a molecule sweeps out an area given by twice its diameter, as the molecules with which it collides also have diameter d.)Observe that according to the kinetic theory of gases, h is independent of pressure. This was assumed in the derivation of the gas viscosity equation. This property of gas viscosity inspired Maxwell to make the first accurate measurements of gas viscosity.
Also observe that h is proportional to T1/2, i.e., that gas viscosity increases as temperature increases.
Gases and liquids have different frictional mechanisms at the molecular level. This explains differences in the temperature dependence of viscosity.
In gases, molecular collisions transfer momentum between fluid layers. As slower molecules collide with faster molecules, the slower molecules speed up and the faster molecules slow down. This effect is observed very often in ice skating rinks! As temperature increases, the molecules move faster and more momentum is transferred between layers, thereby increasing the viscosity.
![]()
A vivid "thought example" of this situation is to imagine two trains moving on parallel tracks at slightly different speeds with barefoot passengers on the roofs on a hot day. The passengers jump from one train to the other train. The fast train will slow down, and the slow train will speed up, due to momentum transfer. As the temperature of the roof increases and the passengers jump between trains more frequently, there is more momentum transfer and the trains tend to equalize in speed more quickly. Thus, the momentum transfer mechanism predicts that viscosity increases with increasing temperature.
In liquids, friction between fluid layers originates from molecules sliding past each other. The close proximity of molecules in liquids allows molecules to investigate he attraction or repulsion they have for each other, in stark contrast to the "billiard ball" behavior of ideal gas molecules. Strong intermolecular attraction results in large viscosity coefficient values. For example, oil is made of large molecules with substantial attractive forces and hence has a relatively high viscosity. From practical experience, it is known that the viscosity of liquids decreases as temperature increases. This is because the higher kinetic energies overcome the attractive forces of the molecules and allow them to slip past one another with greater ease.
Viscosity governs the rate of fluid transport in many everyday processes. Although Thanksgiving Day is a once-a-year event, examples of viscosity abound on the opulent dinner table. After digesting your delicious meal, answer the following questions.