Principles of NMR Spectroscopy

1. What is NMR Spectroscopy?

NMR is an acronym for Nuclear Magnetic Resonance. NMR spectroscopy is a powerful tool for identifying nuclei based on the interaction of electromagnetic fields with a sample in a magnetic field. The technique has developed from an interesting physical curiosity in the 1940’s into one of the most important methods of spectral identification in chemistry, biochemistry, and medicine.

The goals of these notes are to provide an intuitive understanding of the NMR phenomenon. Underlying concepts will be emphasized over mathematical formalism.

2. Background

2.1 Classical Angular Momentum

Just as linear momentum represents the tendency of an object move in a straight line, angular momentum represents the tendency of an object to move in angular motion or rotate. Since momentum has both a magnitude and a direction, it is a vector quantity. Linear momentum is represented by a vector in the direction of motion. Angular momentum, however, is represented through use of the Right Hand Rule (RHR): when the fingers of the right hand are curled in the direction of circular motion, the thumb points in the direction of the angular momentum vector. Mathematically, this is because the angular momentum vector is the cross-product of the position and linear momentum vectors

(1)

There are two kinds of classical angular momentum: orbital angular momentum and spin angular momentum. Orbital angular momentum is the circular motion of an object about a point, like the earth orbiting about the sun once a year. Spin angular momentum is the spinning motion of an object about its own axis, like the earth spinning about its axis once a day.

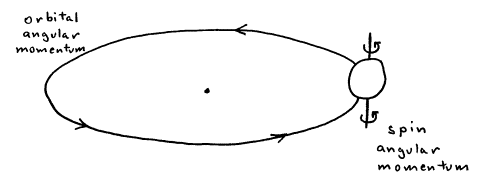
Figure 1. Orbital vs. spin angular momentum.

Exercise 1: Where do the angular momentum vectors lie for each case in Figure 1?

2.2 Quantum Mechanical Angular Momentum

Just as energy is known to be quantized at the atomic level, angular momentum is quantized. For example, an electron in an atom may only have orbital angular momentum quantum numbers l = 0, 1, 2, ... (which are more commonly denoted s, p, d, ...) and orbital magnetic quantum numbers m_l = -l, -l+1, ..., l (which lead to p_x, p_y, and p_z, for l=1 and to the five d orbitals for l=2). Also, the electron only has spin angular momentum quantum number s = 1/2 and spin magnetic quantum numbers m_s = -1/2, 1/2 (which are also known as spin down and spin up).

All types of angular momentum obey the same quantum mechanical rules. In quantum mechanics, an angular momentum vector is restricted to having a magnitude of

(2)

where

L = 0, 1/2, 1, 3/2, ... (3)

is the angular momentum quantum number and

= h/2p (4)

is called “h-bar” and equals Planck’s constant divided by 2p. One component of the angular momentum vector, which is conventionally chosen to be the z‑component, is restricted to having values of

(5)

where

m_L = -L, -L+1, ..., L (6)

is the magnetic quantum number.

Since the magnitude of the angular momentum vector is greater than its maximum projection on the z‑axis

(7)

it is not possible for to lie along the z‑axis. Rather is always tipped away from its quantization axis.

A consequence of the Heisenberg Uncertainty Principle is that only one component of angular momentum can be precisely specified. Defining the z‑component of angular momentum results in the x‑ and y‑components being not well-defined, and the direction in which tips away from the z‑axis is therefore not known. It can be shown that the expectation, or average, values of the x‑ and y‑components of angular momentum are each zero

(8)

A useful picture for representing the different angular momentum quantum states is to imagine 2L+1 vectors with the same quantized magnitudes of but different quantized projections on the z-axis of and undefined projections on the x‑ and y‑axes.

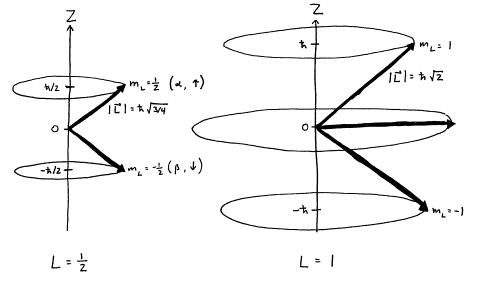
Figure 2. Quantized angular momentum vectors for L=1/2 and L=1.

Exercise 2: Calculate the angle that the L=1/2, m_L=1/2 state lies away from the z‑axis. (Hint: Recall that “cosine equals adjacent over hypotenuse” for a right triangle.)

2.3 Nuclear Spin

Spin is a fundamental property of particles, analogous to mass and charge. It is the angular momentum that is intrinsic to the particle, rather than the angular momentum arising from the overall motion of the particle in space. The spin quantum number I of a nucleus depends on the nuclear species, and has been observed to follow the pattern in Table 1.

Mass Number	Atomic Number	Nuclear Spin (I)	Example
odd	even or odd	1/2, 3/2, 5/2, ...	I(^1H) = 1/2
even	even	0	I(^12C) = 0
even	odd	1, 2, 3, ...	I(^2H) = 1

Table 1. Nuclear Spin Quantum Numbers.

Exercise 3: Observation of an NMR spectrum requires that a nucleus have nonzero spin. Explain why carbon NMR spectra are weak, but still observable. (Hint: The molar mass of natural carbon is 12.011 rather than 12.000.)

Attempts to rationalize the existence of nuclear spin have been made using the model of a spinning charged particle. Classically, it is known that a moving electric charge induces a magnetic field. Since the nucleus has finite diameter and a positive charge, it would generate a magnetic field as it spins about its axis. However, a quantitative analysis of this model yields a value for the intrinsic magnetic field about an electron twice as large as it should be (which is accounted for by the Landé g factor), and the model cannot explain the observation that the spin of an electrically neutral neutron is 1/2 (see the Table 1). While the picture of a spinning nucleus is classically appealing, spin angular momentum is best treated as a quantum mechanical phenomenon.

Figure 3. Classical model of nuclear spin.

2.4 Nuclear Magnetic Moment

The nuclear spin quantum number I gives rise to nuclear spin angular momentum . The nuclear spin angular momentum in turn gives rise to a nuclear magnetic moment according to

(9)

where g is the gyromagnetic ratio (or more correctly the magnetogyric ratio, whose name originates as the ratio of the “magneto” = “magnetic object” over the “gyric” = “turning object”). Each nuclear species has a different value of g, which is experimentally determined.

Since the nuclear magnetic moment vector is directly proportional to the nuclear spin angular momentum vector, the nuclear magnetic moment obeys the same rules of quantization as angular momentum,

(10)

and

(11)

where

m_I = -I, -I+1, ..., I (12)

Exercise 4: Draw a picture of nuclear magnetic moment vectors for I=3/2 analogous to the picture of spin angular momentum vectors in Figure 2. Label the magnitude and z‑projection of each vector.

Nucleus	Spin (I)	Natural Abundance / %	Magnetogyric Ratio (g) / 10^7 kg^-1·s·A	Relative Frequency (n) / MHz
^1H	1/2	99.985	26.752196	100.00
^2H	1	0.015	4.106625	15.35
^13C	1/2	1.10	6.72828	25.15
^15N	1/2	0.366	-2.712621	10.14
^17O	5/2	0.037	-3.62808	13.56
^19F	1/2	100.0	25.18147	94.13
^29Si	1/2	4.67	-5.319	19.88
^31P	1/2	100.0	10.8394	40.52
^119Sn	1/2	8.58	-10.0318	37.27

Table 2. Spin, natural abundance, magnetogyric ratio, and relative frequency for some common NMR nuclei.

Exercise 5: Calculate m_z for a single proton with m_I=1/2 in SI units. (Hint: The quantum number I is unitless, and J = kg·m²·s^-2.) [Answer: m_z = 1.4106´10^-26 m²·A]

3. Effect of a Magnetic Field

3.1 Nuclear Energy Levels

In the absence of external fields, there is no preferred orientation for a magnetic moment. In the presence of a magnetic field , however, the energy of a magnetic moment depends on its orientation relative to the field lines. Classically,

(13)

The energy is a minimum when the magnetic moment is aligned parallel to the magnetic field and a maximum when it is anti-parallel to the magnetic field.

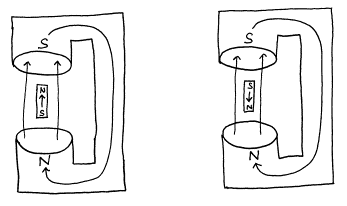
Figure 4. Low energy and high energy configuration of a magnet in an external field.

The energies of the above two cases may be calculated to be

E_low = -m B₀ (14)

and

E_high = m B₀ (15)

where m is the magnetic moment and B₀ is the external magnetic field strength.

The energy of a magnet at an arbitrary orientation between these limits is calculated by multiplying the projection of the magnetic moment along the field direction by the field strength. Assuming that the quantization axis is taken to be the direction of the magnetic field, then the energy of the m_I nuclear spin state is

(16)

from which it is seen that the energies of different m_I states of a nucleus are not degenerate in an external magnetic field. Hence, the m quantum number is called the magnetic quantum number.

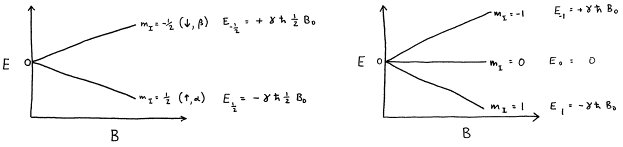
Figure 5. Energy levels for I=1/2 and I=1 as a function of magnetic field strength. (The relative scale of the diagrams is arbitrary, as different nuclear species have different values of g.)

Exercise 6: Calculate E for a m_I=1/2 proton in a 1.41 T field. (Hint: T = V·s·m^-2)

3.2 Boltzmann Distribution

In the presence of an external magnetic field, different m_I nuclear spin states have different energies. At thermal equilibrium, they will also have different populations according to the Boltzmann equation

(17)

where N_high and N_low are the populations of the upper and lower states respectively, DE = E_high - E_low is the energy difference between the two states, k is the Boltzmann constant, and T is the absolute temperature.

Exercise 7: Calculate N_high/N_low for protons in a 1.41 T field at 298 K. Calculate N_high/N_low in a 7.05 T field. State the dependence of N_high/N_low on magnetic field strength.

In the limit as T approaches zero (or DE approaches infinity), N_high/N_low approaches zero implying that only N_low is populated. In the limit as T approaches infinity (or DE approaches zero), N_high/N_low approaches unity implying that N_low and N_high are equally populated. In practice, the difference between nuclear spin energy levels DE in achievable fields is much smaller than kT, implying that N_low is only very slightly in excess of N_high.

An analogy to the thermal population of N_low and N_high is a collection of compasses which lie on a table. When the table is undisturbed, all the compasses will be in their low energy state and point toward the earth’s north pole. However, if the table is shaken, then some of the compasses will adopt the higher energy state of pointing toward the south pole. In practice, the thermal energy of shaking vastly exceeds the magnetic force attempting to align the magnets along the earth’s field, resulting in near equal numbers of compasses pointing north and south. Note that the shaking causes the compasses to continually switch directions that they are pointing. Thus the equilibrium between high energy and low energy configurations is a dynamic equilibrium, not a static equilibrium.

Exercise 8: Evaluate the “high temperature approximation” by calculating

(18)

for protons in a 1.41 T field at 298 K and comparing it to the previously calculated exact answer.

3.3 Transition Frequencies

NMR spectroscopy is performed by inducing transitions between adjacent nuclear spin energy states (Dm_I = ±1). The energy change for a nucleus undergoing an NMR transition is

(19)

Equation (19) may be interpreted as follows. The difference between angular momentum z‑component of adjacent m_I states is . This difference is multiplied by g to obtain the difference in the magnetic moment z‑component. This result is then multiplied by the magnetic field strength to obtain the energy difference between adjacent m_I states in a magnetic field.

Exercise 9: Calculate DE for a proton in a 1.41 T field.

The frequency n of the electromagnetic radiation used to induce a NMR transition between adjacent m_I levels in external magnetic field B₀ is calculated from

DE = hn (20)

which yields

n = DE/h = gB₀/h = gB₀/2p (21)

The units of frequency (n) are cycles/second, which are also called Hertz (Hz). In NMR spectroscopy, it is often more convenient to use angular frequency (w) with units of radians/second. Since one cycle equals 2p radians,

w º 2pn (22)

Since cycles and radians are not SI units, both n and w have the same SI units (s^-1). Thus, frequency (cycles/second) and angular frequency (radians/second) must be distinguished through careful use of the symbols of n and w, respectively. The angular frequency of an NMR transition is more commonly written as

w₀ = gB₀ (23)

which is the famous Larmor equation. Note that the use of w eliminates the occurrence of 2p in the Larmor equation.

Exercise 10: Calculate n and w for a proton in a 1.41 T field. In what region of the electromagnetic spectrum does this frequency occur? State why a NMR spectrometer with a 1.41 T magnet is commonly referred to as a “60 MHz spectrometer.”

4. Generation of the NMR Signal

4.1 Overview

The measurement of a NMR spectrum signal is very different from infrared or UV‑VIS spectroscopy in which absorption of photons is measured as a function of frequency. It has been argued that NMR spectroscopy is similar to emission spectroscopy, in that absorption of radiowave frequencies is detected indirectly by the subsequent emission of radiowaves at the same frequency. While this explanation can account for a simple proton NMR spectrum, it does not readily explain pulsed experiments that have give NMR its tremendous ability to uncover couplings and correlations among nuclei in a molecule. Furthermore, counterarguments have been made that the small NMR probe would be an very poor emitter and receiver of long wavelength radiofrequency radiation and the relatively low radiofrequency implies extremely low absorption and emission probabilities. Hence, it is better to view NMR spectroscopy as a magnetic induction experiment rather than as an experiment involving absorption and emission of photons.

A more complete understanding of NMR spectroscopy is achieved if one considers the effect of applied magnetic fields on the nuclear magnetic moments in the system. Briefly, an NMR sample in an external magnetic field is disturbed from equilibrium by application of a transverse secondary magnetic field, and its response to the disturbance is recorded. Furthermore, a tremendous enhancement of signal-to-noise, as well as the ability to carry out multiple-pulse experiments, occurs when a pulse of radiowave frequencies is used to disturb the system from equilibrium. The time dependence of the return to equilibrium is then measured, from which frequency spectrum is generated via a Fourier transform. In this section the underlying physical basis if the NMR phenomena is described. The implementation details in a modern spectrometer are covered in a subsequent section.

4.2 Net Magnetization Vector

It will be necessary to distinguish between motion relative to the laboratory in which the external magnetic field originates and motion relative to other coordinate systems. The cartesian coordinates associated with the laboratory will be denoted X, Y, and Z. If the magnetic moment vectors of a collection of nuclei are quantized in the direction of the external magnetic field, then they have well-defined projections along the Z‑axis but are randomly distributed in the XY‑plane. Since there is a slight excess of the lower energy projections aligned parallel to the field over the anti-parallel projections, there is a slight net magnetization in the Z direction. However, there is no preference for the X or Y direction so there are equal numbers of projections onto this plane pointing in each direction, resulting in no net magnetization in the XY‑plane. The net magnetization vector is labeled , and may also called the macroscopic magnetization vector or the equilibrium magnetization vector.

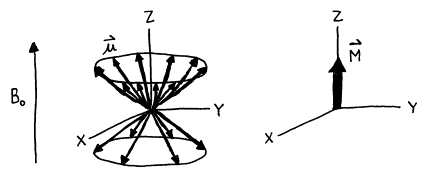
Figure 6. The vector sum of a collection of I=1/2 nuclear magnetic moments in an external magnetic field.

The measurement of the net magnetization vector was a very challenging task due to the small magnitude of the vector and the very large applied field in the same direction. Bloch and Purcell independently made this measurement for the proton in 1946, for which they were jointly awarded the Nobel Prize in physics. However, neither of them would have predicted that organic chemistry students would routinely make such measurements in order to distinguish among the same nuclear species in different chemical environments with differences in magnetic moments of less than 0.1 ppm!

Exercise 11: Calculate the net magnetization of 0.1 mL of water in a 1.41 T magnet at 298K. Compare this value to the earth’s magnetic field strength of approximately 1 gauss. (Hints: Each water molecule contains 2 H atoms, and O has an even number of protons and neutrons. 10⁴ gauss = 1 T.)

4.3 Larmor Precession

When a rapidly spinning gyroscope is tipped from vertical, it does not fall over but rather experiences a torque given byand precesses about the earth’s gravitational field. Careful observation of a gyroscope’s precessional motion reveals that the precessional frequency is independent of tip angle and the tip angle remains constant during precession.

When a magnetic moment lies at an angle to an external magnetic field, it experiences a similar torque

(24)

and it precesses about the external field. The precession frequency is given by the famous Larmor equation

w₀ = gB₀ (23)

and w₀ is the Larmor frequency and B₀ is the external magnetic field strength. The Larmor frequency has two important physical interpretations. It is the precessional frequency of the nuclear magnetic moment about the magnetic field. It is also the frequency of the electromagnetic radiation that induces a transition between nuclear spin quantum states in the magnetic field.

Since each individual nuclear magnetic moment vector is tilted from the external magnetic field, it experiences precessional motion about the Z‑axis. However, as long as the net magnetization vector lies along the Z‑axis, it does not undergo precession.

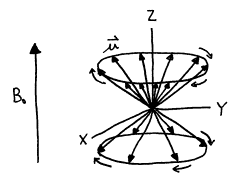
Figure 7. Precession of I=1/2 magnetic moment vectors in applied magnetic field B₀.

4.4 Transverse Magnetic Field

Larmor precession of the magnetization vector is not observed as long as lies in the direction of the magnetic field . In order to observe precession of about , must be tipped away from the Z‑axis. This can be accomplished by introducing another magnetic field that is perpendicular to the Z‑axis.

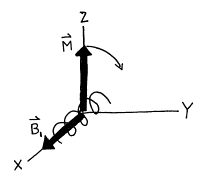
Figure 8. Coils in a NMR spectrometer which tip the magnetization vector M.

In a NMR spectrometer, the field is generated through the use of a solenoid coil of wire whose axis lies in the XY‑plane. We will define the X‑axis to lie along the axis of the coil. If electric current flows through the coils, a magnetic field is generated along the X‑axis, and the magnetic moment is tipped off the Z‑axis toward Y‑axis in accordance with Eq. (24). If were a static field, then would precess about the new overall magnetic field at the Larmor frequency. In an NMR spectrometer, <<; hence, the tip angle of would be minimal and a negligibly small NMR signal would be generated. Furthermore, relaxation effects would ultimately cause to align with the new field, and precession would stop. In short, use of a static field would result in a very uninteresting NMR experiment, as it is equivalent to simply changing the direction of the external magnetic field.

A very different situation arises if is not static but is made to rotate with about the Z‑axis with the Larmor frequency w₀. Then continues to tip away from the Z‑axis toward the XY‑plane so as to precess about the rotating field at Larmor frequency w₁. The overall motion of in this case is quite complex. is a spiral motion on the surface of a sphere, rotating about the Z‑axis at w₀ and away from the Z‑axis at w₁. In this arrangement, the tip angle of away from the Z‑axis can reach a full 90° and thereby generate a significant NMR signal.

Figure 9. Precession of about for stationary and for rotating .

A rotating magnetic field is generated by connecting the coils to a radiofrequency source whose output voltage varies sinusoidally at frequency w₀. An alternating current (AC) will flow in the coil, producing a linearly oscillating magnetic field. The resulting magnetic field is colinear with the X‑axis but varies in magnitude so as increase along the positive X‑axis, reach a maximum, decrease toward zero, increase along the negative X‑axis, reach a maximum in this direction, and return to zero. A linearly oscillating vector can be decomposed into the sum of two counter rotating vectors. Each rotating vector rotates at frequency w₀; however, one vector rotates in the same direction of Larmor precession of and the other in the opposite direction. The component of the magnetic field rotating with is the field. (It turns out that the other component has a negligible effect on the net magnetization vector, as it differs too much in frequency from w₀.)

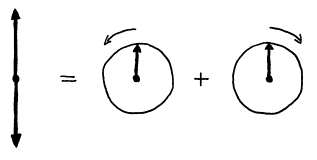
Figure 10. Decomposition of a linearly oscillating magnetic field into two counter rotating magnetic fields.

4.5 Rotating Frame of Reference

In order to simplify the motions of the nuclear magnetic moments during an NMR experiment, a new axis system is introduced which rotates in the same direction and rate as the moments are precessing. The axis system is called the rotating frame, and the axes are labeled with lowercase x, y, and z. Recall that the stationary or laboratory frame axes are labeled with uppercase X, Y, and Z. (Older literature, however, uses x, y, and z for the stationary frame and x', y', and z' for the rotating frame.) Use of the rotating frame allows one to visualize more easily all motion of the magnetic moments other than Larmor precession. An analogy to understand this is to consider reading the label on a record while it is being played on a turntable. It is difficult to read the label while you are stationary and the label is rapidly rotating; however, it would be much easier to read the label if you “jumped aboard” the rotating album and rotated with it, as the label would appear to not move in your new rotating frame. However, note that the label could appear upright, upsidedown, or even sideways, depending on when one jumped aboard the rotating frame.

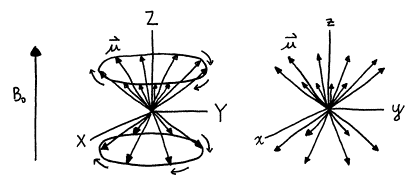
Figure 11. Rotational motion in the laboratory frame appears to stop in the stationary frame.

The motion of the rotating field is quite simple in the rotating frame. Since the rotating frame rotates at exactly the frequency of the vector , the vector is a stationary in the xy‑plane. The motion of the magnetization vector in the rotating field is also very simple. The precessional motion of about the z‑axis at Larmor frequency w₀ stops, and simply precesses about the stationary vector at frequency w₁.

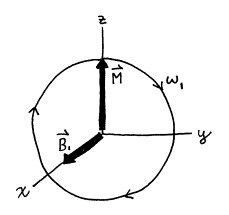
Figure 12. Motion of magnetization vector in rotating frame of reference.

It is quite clear in the rotating frame system that the rotation frequency of must match the Larmor frequency w₀ in order to significantly tip the magnetization vector. Imagine that the vector were rotating slightly slower (or faster) than which rotates at the Larmor frequency w₀. Initially, the field would tip the magnetization vector away from the z‑axis in a particular direction. However, the mismatch between rotation frequency of and the Larmor frequency w₀ would soon cause to precess around the z‑axis to the side opposite of its initial tip. The field would then tip back toward the z‑axis restoring it to its original alignment. The only frequency at which the rotating magnetic field can significantly tip the magnetization vector is the Larmor frequency w₀. Thus, it is an excellent approximation to ignore the component of the linearly oscillating magnetic field that rotates in the opposite sense as , for its rotational frequency is -2w₀ in the rotating frame and its effect on is therefore neglible.

Rotating the axis system at the Larmor precession frequency w₀ is extremely useful. While Larmor precession is a consequence of the external magnetic field that is necessary to generate a NMR signal, it contains no useful information beyond the value of the magnetogyric constant g. Rather, all the interesting information in a NMR spectrum arises from the slightly different magnetic fields that nuclei experience due local environment differences, and this information is contained in the small differences among their Larmor frequencies rather than the total magnitude of the Larmor frequency. It is always easier to see a small signal when it is not on top of a large background. Hence, it is both mathematically convenient and experimentally necessary to reference all NMR signals to the Larmor frequency of the external magnetic field.

If is chosen to lie on the x‑axis, then tips from the z‑axis toward to y‑axis according to Eq. (24). Note that because this is precessional motion, the angle between and (90° in this case) is maintained (motion remains in the yz‑plane in this case). In a pulsed Fourier Transform NMR spectrometer, is it possible to control the direction in which tips, the rate at which tips, and the amount of the tip angle. The field is generated by a short pulse of radiofrequency (RF) into the coils which surround the sample in the probe. The direction of tipping is controlled by the relative phase between the applied radiofrequency pulse and the rotating frame. For example, if the maximum RF intensity occurs when rotating the x‑axis lies along the coil, then the field is along the x‑axis. However, if the maximum RF intensity occurs when the y‑axis lies along the coil, then the field is along the y‑axis. The rate and magnitude of the tip is determined by the RF power and the duration of the RF pulse, respectively. Stronger RF power creates a stronger field that results in a higher w₁, and a longer RF pulse causes the precession about precession to continue further. It is the ability to precisely control the tip of the magnetization vector that makes multiple pulse NMR experiments possible.

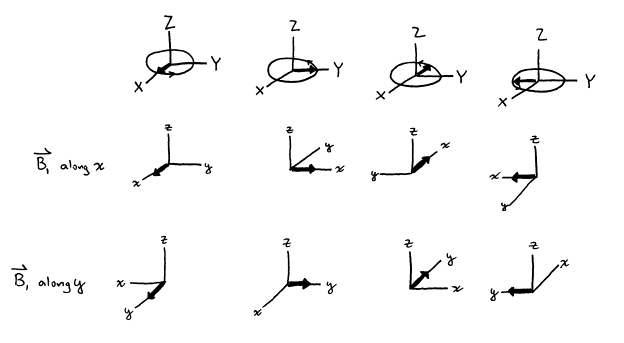
Figure 13. Generation of along the x‑axis and along the y‑axis.

Current convention defines an “x‑pulse” as a pulse that induces rotational of about the x‑axis in a positive or Right Hand Rule sense, i.e., y®z®-y®-z. However, the older literature and many textbooks define an x‑pulse in the opposite sense. As long as either convention is used consistently, it will predict the same result for NMR experiments as the other convention. Since both conventions are widely found, one should not worry about the particular choice made an author but should note the choice and follow it in that article or book. Careful consideration of Eq. (24) and the definition of positive rotation reveals that . Thus, the magnetic field which induces an x‑pulse is actually aligned along the negative x‑axis for a nucleus with a positive magnetogyric ratio. The choice of whether to define an x‑pulse with respect to the rotation vector or the magnetic vector is matter of preference. However, current convention is to focus attention on rotation of the magnetization vector rather than on the radiofrequency magnetic field vector. This is known as the Right Hand Convention, because if one aligns the thumb of the right hand along the axis of the pulse, the fingers curl in the direction that rotates.

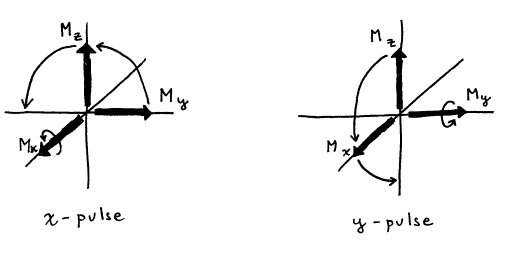
Figure 14. The effect of an x‑pulse and a y‑pulse on the magnetization vector components

Exercise 12: What is n₁ for a 10 ms pulse that rotates by 90° for a proton? What field strength is required for this pulse? Compare the strength of to for this case in a 300 MHz NMR spectrometer? [Answers: 25kHz; 5.87 gauss; 12000:1]

Exercise 13: A typical RF coil in a probe consists of 2 turns of wire with 1 cm radius separated by 1 cm and has an impedance of 50 ohms. How much power must be delivered to the probe to produce the above 90 degree pulse? (Hints: A general physics textbook calculation reveals 1 A of current in a 1 loop coil with 1 cm radius produces a 6´10^-5 T magnetic field. P=VI=I²R.)

We will later see that the rotating frame is more than a mathematical construct to assist in the visualization of motion of nuclear magnet moments. The rotating frame is actually the reference signal to the Phase Sensitive Detector in the NMR spectrometer!

4.6 Observation of the NMR Signal

Just as an oscillating electric field in a coil of wire creates an oscillating magnetic field, an oscillating magnetic field causes an oscillating electric field in the wire. The alternator found in every automobile operates on this principle. The NMR signal is observed with a coil in the XY‑plane similar to the transmitter coil that detects the rotating magnetization vector . Early NMR spectrometer designs used separate transmitter and receiver coils; however, modern designs use a single transceiver coil that is electronically connected to the transmitter during the pulse and then to the receiver after the pulse. Although is stationary in the rotating frame, it is moving at the Larmor frequency in the stationary frame. As , the projection of on the xy‑plane, cuts through the turns of the received coil, it induces a RF current at frequency w₀. The spectrometer looks for an electrical signal at w₀ in the receiver coil, typically by comparing the output signal to the input signal with a Phase Sensitive Detector as discussed in a subsequent section.

Observation of the NMR signal requires that the magnetization vector be tipped toward the xy‑plane. This tipping only occurs when the transverse field rotates at the same frequency as the Larmor precession frequency w₀, i.e., when the RF transmitter frequency is tuned to the Larmor frequency. The transfer of RF electrical energy into tipping of the magnetization vector relies on a close match between the applied RF frequency and Larmor precession frequency. The physical phenomenon of two oscillating systems transferring energy most efficiently when their frequencies are the same is called resonance. Hence the name nuclear magnetic resonance is a very appropriate term to describe the frequency dependence of coupling RF electrical signal into the tipping of the magnetic moment vector.

Optional Exercise 14: Estimate the NMR signal power (in watts) of a 0.1 mL water sample in a 1.41 T magnet (exercise 11) observed with a typical RF probe (exercise 13).

4.7 Relaxation

The relaxation of net magnetization vector has been ignored until now. Recall that the equilibrium which produces is a dynamic equilibrium and that thermal energy constantly causes transitions between nuclear spin states. The equilibrium population among the nuclear spins states is determined by the Boltzmann distribution. When the system is perturbed from equilibrium by application of , it will relax back toward equilibrium. The specific mechanisms for relaxation are quite complex and will be discussed in a later section. Factors that affect the relaxation rate include nuclear species, magnetic field homogeneity, temperature, and presence of magnetic material (ranging from other nuclei with spin to paramagnetic species such as a dilute aqueous CuSO₄ solution).

If is tipped by a short pulse of radiofrequency, it will commonly take several seconds for to return to its equilibrium position along the z‑axis. Two distinct kinds of relaxation occur, each with its own time constant. Relaxation of along the z‑axis occurs with time constant T₁, which typically varies from seconds for protons to tens of seconds for carbon. Since T₁ is a measure of the time required for magnetization vector to return to its equilibrium length and direction, it directly affects when the next radiofrequency pulse can be applied. The delay before applying the next pulse can vary from zero to 5 T₁, depending on the specific experiment being carried out. Relaxation of the vector magnitude in the xy‑plane occurs with time constant T₂*, which is typically on the order of a second or two. Since T₂* is a measure of the time required for the magnetization vector to leave the xy‑plane, it is a direct measure of the length during which a signal can be observed. The magnitude of T₂* therefore affects the length for which a FID should be recorded. A general guideline is to collect the FID for 3 to 4 T₂*.

4.8 Factors Affecting Sensitivity

The NMR signal depends linearly on the magnitude of magnetization in the xy‑plane, . This quantity is governed by four factors for a given nucleus. First, the tip angle of the magnetization vector affects . The closer the tip angle is to 90°, the larger the magnitude of the magnitization vector is in the xy‑plane. Second, the external magnetic field strength affects the magnitude the magnetization vector , and consequently its projection in the xy‑plane. Third, the sample temperature also affects magnetization vector , as a colder sample results in a larger population difference between spin states. Fourth, the number of nuclei in the coil, which is usually controlled by sample concentration, also directly affects the magnetization vector .

The NMR signal also depends on the magnetogyric ratio g raised to the third power. This strong dependence arises from the magnetic moment depending linearly on g, the population difference between spin states depending linearly on g, and the efficiency of signal generation depending on the Larmor frequency w, which is proportional to g.

Exercise 15: Estimate the relative sensitivity of ¹H and ¹³C NMR spectra. (Hint: account for relative abundance, relaxation, and magnetogyric ratio.)

5. Chemical Shift

5.1 Different Nuclei (magnetogyric ratio)

According to the Larmor equation, the precessional frequency of a nuclear magnetic moment is proportional to the magnetogyric ratio and the magnet strength.

w₀ = gB₀ (23)

Different nuclei have different magnetogyric ratios (see Table 2). Thus for a given magnetic strength, the frequency at which nuclei of different elements precess depends on their identity and differs vastly.

It is common practice to characterize magnet strength by a precessional frequency, e.g., a 300 MHz magnet. Such terminology assumes a specific nucleus, typically a proton. Thus in a 300 MHz spectrometer (for protons), the precessional frequency of carbon is 75 MHz.

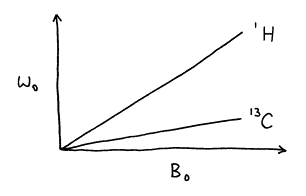
Figure 15. Dependence of precessional frequency on magnet strength on the magnetogyric ratio.

5.2 Inequivalent Nuclei (shielding)

All atoms in a molecule are surrounded by electrons that occupy core and valence orbitals. The permanent magnetic field induces a current in the surrounding electrons, which in turn generates an induced magnetic field . According to Lenz’s Law, the induced field is proportional to the permanent magnetic field but is opposite in direction

= -s (25)

where the proportionality factor s is called the shielding constant.

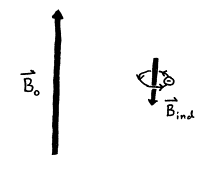
Figure 16. Electrical current flow from surrounding electrons induces to oppose .

The local magnetic field experienced by a nucleus is the sum of the permanent field and the induced field

= + (26)

Nuclei in different chemical environments are called inequivalent nuclei, and they experience slightly different local fields and therefore precess at slightly different Larmor frequencies

w₀ = g B_loc = g (B₀ + B_ind) = g (B₀ - s B₀) = g B₀ (1 - s) (27)

Nuclear magnetic resonance frequencies are always reported with respect to a standard. The standard for protons and for carbon is tetramethylsilane (TMS), Si(CH₃)₄. If the frequency difference is reported in Hertz, then it is proportional the external field strength. Given nucleus A and standard B with Larmor frequencies w_A and w_B, the chemical shift of A with respect to B is

n_A-n_B = (w_A-w_B) / 2p = [g B₀ (1- s_A) / 2p] - [g B₀ (1- s_B) / 2p] = g B₀ (s_B- s_A) / 2p (28)

Thus, the energy spacing between two inequivalent nuclei is proportional to magnetic field strength B₀. This increase in spectral separation with field strength is one of the main advantages of using higher strength magnets in modern NMR spectrometers. (The other advantage is the higher sensitivity achieved due to the greater population difference between spin states.)

It would be quite inconvenient to report nuclear magnetic resonance frequency differences in Hertz because the strength of every magnetic is different. Dividing by the frequency of a standard, which is also dependent on field strength, eliminates this dependence on magnetic field strength.

(29)

since s_B<<1. The chemical shift in parts per million d of nucleus A is the usual quantity reported in the literature.

(30)

As will be seen in future sections, however, it can also be useful to think about the chemical shift relative to the standard in Hertz, especially when considering Fourier Transform NMR and spin-spin coupling strengths.

Dn = n_A-n_B (31)

In general, the amount of shielding is proportional to the local electron density, i.e., higher electron density causes more shielding and results a lower Larmor frequency. However, it is possible for some chemical groups with circular p electron systems, most notably aromatic rings and triple bonds, to cause induce chemical shifts which are not the same for all orientations in space, a phenomenon known as chemical shift anisotropy.

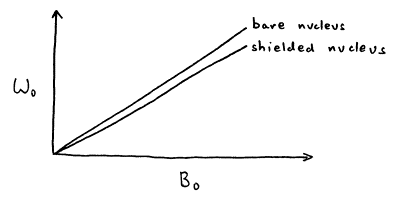
Figure 17. Shielded nucleus has a lower Larmor frequency.

Figure 18. Induced field can cause chemical shift anisotropy.

Exercise 16: Consider the proton in chloroform, Cl₃CH, and the chemically equivalent protons in tetramethylsilane (TMS), Si(CH₃)₄. Which proton has the higher Larmor frequency? Explain your reasoning. (Hint: Consider the electronegativity of the other atoms in each molecule.) [Answer: Chlorine is more electronegative than silicon. Thus, the proton in chloroform is less shielded and has a higher Larmor frequency.]

Exercise 17: The CHCl₃ proton resonance is observed at 436 Hz in a 60 MHz spectrometer and at 2181 Hz in a 300 MHz spectrometer relative to TMS. Calculate the chemical shift d in ppm in each case. [Answer: 7.27 ppm in each case]

5.3 Equivalent Nuclei (spin-spin coupling)

Nuclei with spin can interact, or couple, with each other. Since each nucleus can be thought of as a small magnet, the orientation of that magnet has an effect on the local magnetic field experienced by other nuclei. This effect is most prominent among chemically equivalent nuclei, giving rise to the N+1 rule for equivalent protons learned in organic chemistry. A proton with N protons on contiguous carbon atoms splits into N+1 peaks with intensity pattern given by 1:1, 1:2:1, 1:3:3:1, ... for N equal to 1, 2, 3, ... Spin-spin coupling will be discussed in much greater detail in a future section, with extensions to more complicated interactions including interactions between different nuclei.

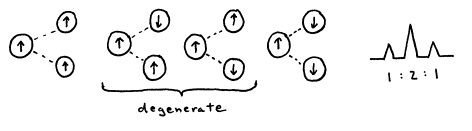
Figure 19. 1:2:1 intensity pattern arises from one proton coupling with two equivalent protons.

Exercise 18: Qualitatively predict the chemical shift and spin coupling pattern of the ethyl group, CH₂CH₃, in ethanol, HOCH₂CH₃. Justify your assignments.

---